福 田 洋 一*
京都大学大学院理学研究科
(1999年11月12日受付,1999年12月10日改訂,1999年12月13日受理)
Satellite altimetry and Satellite Gravity Missions
Yoichi Fukuda
Department of Geophysics, Graduate School of Science, Kyoto University
Kitashirakawa Oiwake-cho, Sakyo-ku, Kyoto, 606-8502, Japan
(Received November 12, 1999; Revised December 10,1999; Accepted December 13, 1999)
Abstract
*E-mail : fukuda@kugi.kyoto-u.ac.jp, Fax:075-753-3912
1.はじめに
衛星アルティメトリィとは,人工衛星に搭載されてマイクロ波レーダ高度計(通常,衛星高度計,海面高度計,あるいは単にアルティメーターなどと呼ばれているが,ここでは,以後,衛星高度計と呼ぶことにする)を用いて,人工衛星から海面までの距離を精密に測ることである.このアイディアそのものはかなり古くからあり,既に1973年にSKYLABによって最初のテスト的な測定がなされている.アルティメトリィの成果については後に詳しく述べるが,このような単純なアイディアの測距技術が,近年の海洋での重力場の研究に一大革命をもたらすとともに,現在では,海洋学の研究に欠くことのできない観測手段となっている.一方,衛星重力ミッションは,衛星軌道から地球の重力場を直接測る計画で,現在,既に,2000年にCHAMP (CHAllenging Mini-Satellite Payload),2001年に GRACE(Gravity Recovery and Climate Experiment)の打ち上げが決まっている.さらに, 2004年の打ち上げを目指してGOCE(Gravity field and Ocean Circulation Explorer) 計画が進行中である.衛星高度計と重力ミッションの間には,一見,直接的な関係はないように思われるかもしれない.しかしながら,衛星アルティメトリィから衛星重力ミッションへのながれは,地球科学的な必然性からの要請であり,実際,1990年台の衛星アルティメトリィは,当初,衛星重力ミッションの実現を前提として計画されていたように思われる.それが,種々の事情で,衛星重力ミッションの実現だけが遅れたということである.
衛星重力ミッションの実現は,10年近く遅れてしまったものの,この間の地球科学の発展や各種のデータの蓄積,また,測定技術や精度の格段の進歩によって,以前は考えもおよばなかった新しい応用分野が開けようとしている.すなわち,従来の衛星重力ミッションが,単に,静的な地球重力場の精度向上を目指していたのに対して,現在計画されている重力ミッションでは,重力場の時間的な変化の検出をも一つの重要な目的としている.例えば,GRACEの主要な研究課題の一つに,海洋,大気(水蒸気),陸水間でのグローバルな水循環に伴って生じる質量移動を重力の時間的変化として検出しようとするものがあるが,このアイディアを発展させると,地球上で生じている質量の移動を伴うさまざまな現象は,少なくとも原理的には,すべて重力変化として検出できることになる.このような発想は,現在計画されている衛星重力ミッションでの重力場の測定精度を考えると,夢物語とばかりは言えないほど現実味をおびてきており,これらの衛星重力ミッションが実現した際には,従来考えられなかった地球科学の全く新しい研究分野を切り開く可能性さえ持つに至っている.
本稿の主な目的は,衛星アルティメトリィならびに衛星重力ミッションについて,測地学的,地球科学的な意義に重点を置きながら,その一般的な紹介をすることであるが,同時に,このような衛星観測に何が期待され,何が実現して来たかを概観することにより,今後の重力場研究の方向性を考える一助となれば幸いである.
2.衛星アルティメトリィ
2.1.海面高測定とは
Fig.1は,衛星高度計による海面高測定の様子を模式的に示したものである.先に述べたように,衛星高度計によって得られるデータは,人工衛星から海面までの正確な距離であり,その測定精度は,現在では,1〜2cm程度にも達している.今,衛星の軌道は地球の重心に対して十分な精度で得られているものと仮定する.次に,海には波や海流,あるいは潮汐などの運動はなく,海面は完全に静止していると仮定する.このような海面は,地球重力場における一つの等ポテンシャル面であり,この時,衛星高度計による海面高測定は,海洋における重力場の等ポテンシャル面,すなわち,ジオイドの形状そのものを与えることになる.
これは衛星高度計の測地学的利用におけるもっとも基本的な原理のひとつであるが,このことは測地学の研究にとって2つの重要な意味を持っている.まず第1は,現実面での成果であり、従来、取得が困難であって海域重力場データについて,衛星高度計を利用することで、まず海域のジオイドが,さらに、それをもとにして従来考えもつかなかった詳細な重力異常図が作られるようになったことである(例えば,Sandwell and Smith, 1997).これは,また,結果として地球全体の重力場モデルの改良にも大きく寄与している.
第2の点は,幾つかの仮定はあるにせよ衛星高度計の測定によりジオイドの形状が直接測定可能であるということが初めて示されたことであり,このことは物理測地学の基本理念に大きな変革をもたらした.従来の物理測地学の理論体系は,すべて,地球表面での重力測定データから如何にジオイドの形状を決めるかということに終始していたが(例えば,Heiskanen and Moriz, 1967),衛星高度計の出現で,ジオイド高が直接測定可能であることが現実の測定データによって示された.これにより,最小二乗コロケーション法のように,ジオイド高も重力異常などと同等に重力場の一つの観測量として扱う理論体系が、実際面においてもその真価を発揮することになる(福田,1995).ジオイド高の直接測定は,現在では,地上においてもGPS/水準ジオイド(例えば,Fukuda et al., 1997)として実現されているが,このような発想を実現せしめたという意味での衛星高度計の意義は極めて大きいと考える.
次に,上述の海面が完全に静止しているという仮定をはずし,より現実的な海洋について考えてみよう.現実の海洋は種々の原因で,さまざまな時間スケール,空間スケールで変動しているので,衛星高度計で測定される海面高は,上記のジオイドの形状に,測定時におけるこのような海面の変動成分が加わったものと考えることができる.このような変動成分としては,例えば,海洋潮汐や黒潮などの海流,あるいは,経年的な海水順変動なども含まれる.これらの詳細については後述するとして,ここで注意すべきことは,このような変動成分の大きさは高々1mのオーダーであり,地球上でのジオイド高の振幅(±100m)の1%程度に過ぎないことである.衛星高度計のデータが,まず重力場の研究に貢献したのは,まさにこのためである.一方,現在の衛星高度計の測定精度は,衛星の軌道決定,その他,さまざまな測定誤差を考慮したとしても数cmのレベルにまで達しており,海洋変動の研究にも十分耐えられるようになっている.むしろ,現在の衛星高度計による研究の主流は,このような海洋変動とそれに関連した現象に移っており,また,重力場研究の立場からも,より高精度な重力場の推定の為には,これらの影響が無視できなくなっている.さらに,衛星高度計データでとらえた海洋変動成分による重力場への影響なども研究されるようになってきている.
衛星高度計を利用した研究としては,上述のごとく,海域の重力場の推定と海洋の運動に関連したものに大別することができる.また,前者は衛星高度計データの静的な利用,後者は動的な利用と考えてよく,以下もほぼこの分類に従って,衛星高度計データ利用の詳細について述べる.しかしながら,このような分類はあくまでも便宜的なものであり,静的な重力場の研究においても海洋のダイナミクスの考慮は不可欠であるし,また,動的な研究においても高精度の静的重力場モデルが要求されるなど,それぞれの研究がお互いに関連しあっている点に改めて注意をしておく.
2.2.海域のジオイド・重力異常の研究
2.2.1.GEOS-3
先に述べたように,測地学における衛星高度計の最大の貢献は海域重力場の決定にある.衛星高度計が出現する以前は,海洋の重力場の研究は, 観測船からの船上重力測定に頼らざるを得なかった.しかし,観測船による測定は決して能率的とは言えず,海洋の重力分布は,一部の海域を除き,長い間,ほとんど明らかにされていないのが実状であった.
GEOS-3 (Geodynamics Experimental Ocean Satellite)は,このような状況のもと,海域での重力場の研究を主要な目的として1975年に打ち上げられ,3年以上の長期にわたり,高度計による初の実用的なデータを得ることに成功した.重力測定データの不十分であった当時としては,海域のジオイド分布を知ること自体,一つの重要な研究テーマであり,GEOS-3により,数10cm〜1m程度の精度であれ,ほぼ全世界の海域のジオイド分布が明らかにされたことは,全くの驚異であった.
GEOS-3 Missionの概要については,1979年のJGR (Journal of Geophysical Research)特集号にまとめられているが,同特集号には,海域ジオイドや重力異常の決定に関する問題は当然として(Rapp, 1979),ジオイド高異常から直接地下の密度構造モデリングを行う方法や,海域テクトニクスの研究への応用など,高度計の測定精度の違いはあれ,現在でも通用する研究が多くなされており,GEOS-3によって,海域の重力場の研究における衛星高度計の有効性は完全に実証されたように思われる.
2.2.2.SEASAT
GEOS-3に引き続き,1978年には海洋観測を主要な目的としてSEASATが打ち上げられた.SEASATには,5種類のセンサーが搭載されていたが,その一つとして公称精度±10cmと,GEOS-3よりはるかに高精度のマイクロ波高度計が搭載された.SEASATによる観測は,残念ながら,電源装置の不良で,約3カ月間と短命に終わったが,それにもかかわらず,SEASATは,初の本格的な海洋観測衛星として多くの成果をあげている.
海域の重力場の研究からみたSEASATの意義としては,まず第1に,高度計の測定精度の高さがあげられる.重力異常の研究に重要なのは,空間的なデータ分布と共に,短波長域での精度,とりわけ,高度計そのものの精度であり,GEOS-3のそれが±50cmであったことに比べると,SEASATの公称±10cmの測定精度は大変な進歩であった.また,第2の点として,衛星の軌道傾斜角が108度と,GEOS-3の115度に比べ,より高緯度でのデータが取得できたことである.SEASATの寿命が短かったため,残念ながら,南極海でのデータは海氷の張り出した冬季のものしか得られていないが,それでも,この貴重なデータを用いて,南極大陸周辺のジオイド高(Segawa and Asaoka, 1982)や重力異常(Segawa et al.,1984)のマッピングが為された.南極大陸周辺は,他の海域と比べ,はるかに船上観測の困難な海域であり,SEASATによる海面高データは,それだけ意義のあるものであった.
1970年代の後半にGEOS-3,SEASATが相次いで打ち上げられた後,高度計を搭載した衛星の打ち上げは,1985年のGEOSATまでしばらく途絶えていた.しかし,この間に,GEOS-3ならびにSEASATで得られたデータの解析が着々と進められており(Rowlands, 1981; Liang, 1983; Sandwell, 1984; Rapp, 1985),海域の重力異常分布に関する研究は大いに進展した.これらのデータは,世界各地でローカルな海域ジオイドや重力異常の研究に用いられ,また,1980年代の中頃以降は,それを用い,複数の研究者によって,グローバルな海域の重力異常図が公表されている(Haxby 1987; Segawa and Matsumoto, 1987).
このようにして,海域での重力異常が明らかになるにつれ,これらの成果を含めることにより,グローバルな地球重力場の球関数モデルの改良も大いに進展した(Rapp, 1981; Lerch, 1982).通常,重力場の球関数係数のうち,次数(n)が30〜70以下程度の,低次のものは,地表での重力データを用いなくとも,衛星の軌道追跡データだけから求めることができるが,それより高次の係数については,どうしても地表データを用いる必要がある.さらに,これらの係数を精度良く決める為には,何よりもデータの均質な分布が重要であり,高度計データによる海域の重力異常データが大きな役割を果たした.例えば,1986年に発表されたn=360のOSU-86Fモデル(Rapp and Cruz, 1986)では,そのもととなるデータセットの一部に,GEOS-3およびSEASATの高度計で得られた海域の重力異常の30’平均値が使用されている.また,この後,Rappらによってに発表されているOSU-89 (Rapp and Palvis, 1990),OSU-91A (Rapp et al., 1991)などオハイオ州立大学の一連の重力モデルでも,次に述べるGEOSAT衛星の成果がいち早く取り入れられている.
2.2.3.GEOSAT
1980年代における唯一の高度計搭載衛星であるGEOSAT(GEOdetic SATellite)は,1985年3月に米海軍によって打ち上げられた(Cheney et al., 1986).GEOSATの最初の18カ月間の測定フェイズは,GM(Geodetic Mission)と呼ばれ,海域の重力場の改良を主目的として,すべての海域を出来る限る均質に覆うような軌道が選ばれた.GEOSAT GMのデータは,当初,その軍事的な価値から全面的に機密扱いとされていたが,まず,南緯30度以南の海域のデータが公開され,その後,1995年にはすべてのデータが公開されるに至っている.GEOSAT GMデータの利用については,現在でも重要な研究課題の一つであり,最近の海域重力場の研究の進歩はGEOSAT GMデータに負うところが極めて大きい.例えば,Sandwell and Smith (1997)は,GEOSAT GMとERS-1などのデータを用い,全球的な2分格子上での重力異常データを得ており,さらに,そのデータを元にして地球上全海域の海底地形を推定している.また,最近では,同データの再処理を行い,1分格子上の重力異常データも公表している.
GEOSAT衛星は,GMの終了後,約17日の周期で同じ軌跡に戻るERM(Exact Repeat Mission)と呼ばれる計画に移行し,その後,約3年間にわたってデータの取得に成功している.ERMの主要な目的は,メソ・スケールの海面変動など,海洋学的な研究にあったが,ERMのデータは,同時に,固体地球科学の分野でも広く利用された(例えば,Fukuda et al., 1988).高度計としてのGEOSATは,基本的な設計などSEASATのそれとほとんど変わらないものの,SEASAT以降のさまざまな技術改革で,周辺データの精度の向上や重力場モデルの改良などで,システム全体としての精度は,SEASATのそれと比べて,大きく向上していた.また, GEOSATは,繰り返し軌道による,初の長期データの取得に成功したことで,データのスタッキングによる精度向上や,海面の変動性(variability)を知ることにより,データ処理精度の向上などにも寄与したものと考えられる.
2.2.4.現在の高度計衛星
1989年にその寿命を終えたGEOSATの成功を引き継ぐかたちで,ESA(European Space Agency)が,1991年7月にERS-1(European Remote Sensing satellite)を,1996年には,2号機であるERS-2の打ち上げに成功している. また,アメリカのNASA (National Aeronautics and Space Administration)とフランスのCNES(Centre National d'Etudes Spatiales)は,1992年8月に,共同で,TOPEX/Poseidon(T/P) 衛星を打ち上げ,1998年2月にはU.S. NavyによってGEOSATの後続機であるGEOSAT FOLLOW-ON (GFO)が打ち上げられている.このように,80年代とは一転して1990年代は衛星高度計の時代と呼べるかもしれないが,実は,既に,これらの衛星の主要な目的は,海洋変動などの海洋学的な研究に移行している.これについては後述することにして,ここでは,それぞれの衛星の特徴を簡単にまとめておこう.
ERS-1/2は,高度計センサーそのものはGEOSATなどと同様の1周波タイプのものであるが,その特徴として,従来からの海域の観測に加え,Ice Modeと呼ばれる測定フェーズを用意することで,氷床や陸域など,広い分野での応用を目指していること,また,そのために軌道傾斜角を98.5度と極軌道に近づけることで極域の観測エリアを広げたこと,軌道の繰り返し周期を適宜変更することで,時間分解能と空間分解能という相反する要求にも答えるように配慮したこと,などがあげられる.このようなERS-1/2の高度計データの特徴を生かして,すでに,グローバルな重力異常のマッピングや,南極海の海氷を含むデータの精密な解析などの研究が為されている(例えば,Knudsen and Andersen,1994).
多目的なERSとは対照的に,T/Pは,高度計による海洋観測専用に計画された衛星であり,周期約10日の回帰軌道,衛星高度計としては初の2周波マイクロ波レーダー高度計の搭載,軌道決定精度向上のため高い軌道高度設定など,海面高度の測定精度を向上するためのあらゆる努力が払われた.この結果, T/Pのデータは,打ち上げ前の予想を上回る高い精度を得ることに成功した.
T/Pの成功は,衛星高度計が海洋学の研究に極めて有用あることをはっきりと証明した.衛星高度計は,もはや海洋モンタリングの一つの手法として確立した技術であり,定常的な運用方法が議論される段階に至っている.GFOもこのような流れのなかで,GEOSATのERMの軌道を正確に継承することで,海洋の変動の研究に焦点を絞って運用が予定されている.
海域の重力場の研究の立場からは,しかしながら,T/Pのデータをはじめ,海洋観測に主眼をおいた繰り返し軌道の衛星高度計データでは,空間的なデータのカバレージの点で,必ずしも満足のいくものではない.また,T/Pでの比較的低角の軌道傾斜角設定は,極域でのデータ取得の点でも不利な条件となっている.従って,固体地球科学でのT/Pデータの利用としては,重力場そのものの直接的な研究と言うよりは,むしろ,その高かい測定精度を生かし,ERS-1/2をはじめとする他の高度計データの処理精度の向上(特に軌道補正)をはかることや,後述する海洋潮汐や海面変動の固体地球におよぼす影響の研究など,間接的な利用に重点が置かれている.このことは,否定的にとらえるのではなく,固体地球科学における高度計データ利用の新たな道を開くこととして肯定的にとらえることも重要であろう.
2.3.海洋変動の研究
地球重力場の研究に果たしたGEOSAT GMデータの役割については既に述べたとおりであるが,GEOSAT ERMは海洋学の研究に与えたインパクトは,それに勝るとも劣らない.GEOSAT ERMの主要な目的は,衛星の同じ軌道下の海面高の変動を,ある時間間隔(GEOSAT ERMの場合は約17日)で繰り返し観測することにより,海洋の変動を連続的にモニターしようというものである.実は,この発想そのものは,SEASATからのものであるが,GEOSATは,空間波長数1000km,周期数ヶ月程度の中間規模の海洋変動の研究に衛星アルティメータが極めて有効であることを初めて実証することに成功した.これは,その後の衛星高度計観測に大きく影響しており, T/P衛星はこの方向性を決定付けるものであった.
海洋がさまざまなスケールで変動していることは明らかであるが,特にT/Pの衛星高度計では,当初の目的であったメソ・スケールの海洋変動に加え,その他,海洋潮汐モデルの改良や,より長期的な海水準変動のモニタリング(例えば,Nerem et al., 1997 )にも衛星高度計データが有効であることを証明した.なお,T/Pのメソ・スケール海洋変動などの純海洋学的成果は,極めて膨大かつ多岐にわたっているので,ここではこれ以上詳しく触れないが,例えば,AVISO(Archiving Validating and interpretation of Satellite Oceanographic data)のNewsletterや関連Webサイトなどから,多くの最新情報を得ることができる.
2.3.1.海洋潮汐の研究
海洋潮汐による海面高変動は,衛星高度計観測の本来の目的からすると,通常ノイズと見なされており,高度計データには,その影響を補正するために必要な海洋潮汐モデルが添付されている.ところで,このことは視点をかえると,海面高度計のデータそのものからも海洋潮汐の影響を抽出できることを示している.
T/Pなどの繰り返し測定の衛星高度計では,その軌道の繰り返し周期をどのように設定するかは,海洋潮汐の影響を考える上で,極めて重要な問題である.例えば,適当な軌道繰り返し周期の設定を行うことで,ある分潮に対する潮汐の影響を全く受けないようにすることも可能であるが,一方,このような設定では,海面高度計データから海洋潮汐の影響を抽出することは不可能である.このため,例えばT/Pミッションでは,衛星の繰り返し周期によるデータサンプリングで,潮汐の主要分潮についてのエイリアシング周期が適当な観測期間で解析可能な程度になるように設定し,高度計データそのものからも海洋潮汐の研究が可能になるように計画された.このようにして,ある程度データが蓄積された段階で,衛星高度計のデータから海洋潮汐モデルを構築し,新しく得られた精度の良い海洋潮汐モデルを用い,海面高データの補正を過去にさかのぼって行うというものである.この計画は見事に成功し,T/Pミッションによって,そのデータを取り込んだ海洋潮汐の研究が集中的に実施され,次々と高精度の海洋潮汐モデルが提唱されるに至っている(例えば,Matsumoto et al., 1995).これらの成果は,高度計データの補正に用いられるようになったことは言うまでもないが,高精度な海洋潮汐モデルを必要とする重力潮汐など,固体地球の研究にも大きく貢献している.
2.3.2.海水準変動
地球温暖化の問題とも関連して,海水準の長期的な変動には社会的に大きな関心が寄せられており,衛星高度計でも,その監視を行うことは一つの重要な研究課題と考えられている.このような長期的な海洋変動のモニタリングのためには,長期間に及ぶ同一軌道での観測とともに,同じ測地基準系での精密軌道決定の重要性が強く指摘されている.例えば,衛星の軌道決定の際に用いられるレファレンス・フレームや軌道追跡システムの違いによって生じる見かけの海面変動速度は数mm/year〜10 mm/year以上にも及ぶといわれており(Morel and Willis, 1999),衛星高度計センサーのキャリブレーションとともに,このような座標系の維持が本質的に重要な問題となっている.
海水準変動の長期的なモニターをどのように実現するかは大変難しい問題であるが,現在の一つの典型的な戦略として次のような方法が考えられている.すなわち,まず,利用可能なすべての検潮データと,同じ場所での衛星高度計データを比較し,検潮データによる衛星高度計データのキャリブレーションを行う.このようにしてキャリブレーションが施された衛星高度計データについて,海面高測定値の全球的な平均を求め,長期的な海水準変動のモニターを行うというものである.T/PのScience Working Team(SWT)の会合で報告されている最新の結果によると,このようにして得られた最近の海面上昇の速度は1〜3mm/yr程度と見積もられている.この速度は,上述のレファレンス・フレーム等の違いによって生じる見かけの海面変動速度と同じオーダーであり,この種の観測の難しさがうかがわれる.なお,これらの変動は,表面海水温(Sea Surface Temperature SST)の変化とよい相関を持っており,その大部分が海水の熱膨張によるものと考えられる.
2.4.今後の衛星高度計計画
T/Pの後継機として,現在,西暦2000年の秋に,Jason-1の打ち上げが予定されている.Jasonは,CNESとNASAが中心となって進めているプロジェクトの名称で,T/Pと同一軌道で継続して海面高度の観測を行い,メソ・スケールの海洋変動の研究とともに業務的な海洋変動予測や長期的な海水準変動のモニターなども目的としている.Jason-1はその第1号機で,CNESが開発したPoseidonの発展形の二周波のソリッドステート・レーダー海面高度計やDORISの軌道追跡システム,NASAが開発した水蒸気電波遅延補正の為の三周波の放射計や精密軌道決定のためのGPS受信機などが搭載される.軌道追跡システムとしては上記のDORIS,GPSに加えSLRなどを複合して用い,さらに後述のCHAMPによる重力場測定データも取り入れた新しい重力場モデルを用いることで,最終的に1cmより良い軌道精度を目標としている.この結果,最終的な海面高の精度は, rmsで2.5 cmより良いと言われている.Jasson-1の一つの特徴は,データの速報性を重視している点で,軌道誤差は大きくなるものの,データの取得後,インターネットなどを通じて速報値を出来る限り早く公表し,これらは,海況予報などの現業目的で利用される予定である.
Jason-1に続く衛星高度計として,CNESはJason-2を計画しており,2004年頃の打ち上げを目指している.Jason-2計画にはNASAも強い関心を持っているが,従来のように共同で運行するかどうかはまだ決定されていない.そうはいうものの,NASAではJason-2 への搭載を目指してwide-swath高度計と呼ばれる新しいタイプの衛星高度計を計画中である.従来の衛星高度計が衛星直下の海面高しか計測できなかったのに対して,wide-swath高度計では,衛星から両側に長く張り出した二つのアンテナを使い,互いの海面反射波の干渉を用いて,衛星軌道の両側約200 km程度の幅について,海面高度の面的な測定が可能である.この方法では衛星のロールが測定精度に大きく影響するため,単独の観測では50 cm程度の精度しか得られないものの,同時に搭載される従来型の高度計のデータも用いて,いわゆる軌道交点補正の方法によって衛星の姿勢に関する補正処理を行うことで,最終的には2 cm程度の海面測定精度が得られるといわれており,空間的に密なデータが要求される重力場の研究にも大いに寄与することが期待される.
さらに,現在計画段階のものとしては,ジョンズ・ホプキンズ大のWITTEXと呼ばれる小電力,軽量の小型の衛星を複数個同一のロケットで打ち上げ,同時観測によって時間・空間分解能を向上させる計画や,また,CNESのKaバンドを使った高度計で氷海,氷床や沿岸域などの精度向上をねらった計画,やや毛色の違うものとしては, GPS衛星からの電波の海面での後方散乱波と直接伝達波とを低軌道高度衛星で受信し,その時間差から海面高度を測定しようとするGPSアルティメトリィーの計画(Zuffada et al., 1999)など,興味深いものが目白押しである.これらの計画は,次に述べる衛星重力ミッションと連動して考えるとき,まさにその真価を発揮するものと期待される.
3.衛星重力測定ミッション
3.1.力学的海面高度とジオイド
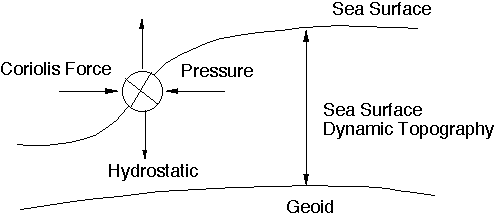
海洋物理学における衛星高度計データ利用の基本的なアイデアは,力学的海面高度と呼ばれるジオイド(ある等ポテンシャル面)から海面までの距離を計測することにある.このような海面の形状は,Fig.2に示すように海流とコリオリ力がバランスしてできるものであり,もしこの力学的海面高度が得られれば,地衡流の仮定によって海面形状の勾配から海流の流速を得ることができる.以上の議論からも明らかなように,海洋学での衛星高度計データの利用に際しては,海域のジオイドを知ることが本質的に重要である.しかも,ここで必要なジオイドは衛星高度計データとは独立な重力測定データから得られるジオイドである.しかしながら,既に述べたように,海域の重力場の研究に衛星高度計が利用されているという状況で,現在の海域ジオイドの精度は,海洋学の研究にとって決して十分とは言えない.例えば,全球的な精度比較において,現在もっとも高精度な球関数重力モデルであるEGM96(Lemoine et al., 1998)でも,海洋のシグナルとのS/N比が1を上回るのは,せいぜい次数にして10数次までの長周期の領域に限られている.衛星重力測定ミッションの一つの重要な目的は,海洋学的研究にも耐え得る高精度なジオイドを提供することである.
海域重力ジオイドの不確かさにも関わらず,既に紹介したように,衛星高度計データが海洋学の研究に盛んに利用されている理由は,これらの研究が,ジオイドの絶対値を必要としない比較的周期の早い時間変動場に絞られているからである.このような問題では,ある仮想的な基準面からの変動成分だけを用いることができるので,特にジオイドの絶対的な形状そのものは必要としない.従来の衛星高度計データは,このように限られた条件でさえ海洋学的に多くの成果を生み出してきたと言える.一方,もしジオイドの形状が正確に知られるようになると,すべての問題で,その絶対値に対して議論が可能になるはずで,その意義は極めて大きいであろう.
3.2.衛星高度計から重力ミッションへ
地球重力場の球関数係数モデルを決める場合,一般に,低次の係数としては衛星の軌道追跡データをもとにした係数を用い,それに,地上での重力データを加えることによって高次の係数を決定している.例えば,上述のEGM96の場合も,次数(n),位数(m)とも70次までの係数について,まず,衛星追跡データだけを用いたEGM96S(SはSatellite onlyの意)モデルがつくられ,それに地表(海域を含む)でのデータを加え,最終的に360次までの球関数係数が決定されている.しかしながら,衛星軌道追跡で得られる重力係数モデルの精度は次数の増加とともに急激に低下し,空間波長数1000 km以下の短波長領域での精度をあげることは極めて困難である.一方,地上での重力データは短波長の精度は確保できるものの,その長波長成分は,データの空間分布の不均質さや,重力測定そのものに由来するバイアス,オフセットなどの問題もあり,波長100km以上の長波長領域での精度は十分でない.現在の重力場データは,このような観測上の問題から空間波長100km〜数1000kmの領域での精度が劣っており,従来の重力ミッションは,弱点であるこの領域での静的な重力場の精度をあげることを第1の目的としていた.
空間波長100km〜数1000kmの領域での重力場の精度向上は,特に,海洋学的な力学的海面高度の研究に決定的に重要である.衛星高度計データによる海面高測定でジオイド面を基準にするかどうかは,ちょうど重力測定における相対測定と絶対測定の関係に似ている.海域のジオイドを基準として海面高度を測ることは,海面高度の絶対測定を意味し,その結果,海面高データから絶対的な海流マッピングも可能になるのである.衛星重力ミッションによる海洋での精密なジオイド決定は,測地学者よりも,むしろ海洋学者から求められていたと言えるであろう.
このような事情で,すでに1980年代の後半には,T/P衛星の計画に際して,出来る限り早期の重力場測定衛星の実現が強く求められており,衛星高度計の計画と平行して,重力偏差計(Gradiometer)を搭載した衛星重力測定計画もすすめられていた.Fig. 3は,1987年にNASAによってまとめられたさまざまな地球科学的研究に必要な静的な重力場の精度(縦軸)と空間波長(横軸)の関係を示した図であるが(NASA, 1987),この図にも重力偏差計の重要性が示されている.Fig.3によると,重力偏差計を搭載した衛星を高度160〜200km程度の低軌道に打ち上げることで,空間波長100kmで重力異常に換算してmgal程度の測定精度が得られ,衛星高度計データと組み合わせることで,これより長波長の海面高の絶対測定が可能となる予定であった.しかしながら,現実にはこのような測定に耐えうる重力偏差計の開発が困難であったことや,経費の問題などもあり,ついに,1990年代には衛星重力測定ミッシュンが実現することはなかった.
重力偏差計を搭載した衛星重力ミッションとしては,現在,ESAによってGOCEミッションが計画されている.GOCEの主要な目的は,静的な重力場の改良にあり,特に,後述するGRACEに比べより短波長での精度向上を目標としており,波長133kmでジオイド高にして0.8cm,80kmでも10cm程度の精度が得られる見込みである.これは,まさに1990年代初頭からの重力偏差計による重力場測定の正当な後継の位置にある.GOCEミッションは,まだ,最終的に打ち上げが決定したわけではないが,最新情報では,2004年7月の打ち上げを目指して準備が進められている.
1990年代の宇宙測地技術の目覚ましい進展については,今更述べるまでもないが,特に,GPSによる測位技術は,精密測位ばかりではなく,電波伝搬遅延を用いた水蒸気分布,大気温度プロファイルの推定,あるいは電離層の電子密度マッピングなど,予想を遙かに越えてその応用分野を拡げている.1990年代に実現できなかった重力偏差計による衛星重力測定は,やはり,まず,GPSによる測位技術の応用としてその実現をCHAMPミッションとして間近に迎えている.また,その後,当面の衛星重力ミッションとしてもっとも期待の大きいGRACEもその技術的な基礎はマイクロ波の干渉測位技術にある.以下,現在,既に打ち上げが決定しているCHAMPミッションならびにGRACEミッションの概要について説明する.
3.3.CHAMPミッション
CHAMPは,ESAが2000年の4月に打ち上げを予定している小型の衛星で,歴史上,初の衛星重力測定とともに,地球磁場の観測とGPSを用いた大気,電離層のサウンディングを行う予定である. この内,CHAMPによる重力場の測定は,いわゆるHigh-Low Satellite-to-Satellite Tracking (H-L SST)と呼ばれているもので(SSTについては,Jekeli and Upadhyay, 1990),高度約300〜400km程度の低高度に打ち上げられた衛星にGPS受信機を搭載し,その軌道位置を高高度のGPS衛星を用いて,連続的に高精度に測定するというものである.この場合,測定データとしては衛星の精密位置が時間関数として得られるので,これを2階微分することにより衛星高度における重力加速度を求めることができる.これを「宇宙空間における自由落下による重力の連続絶対測定」と称したのは,まさに名言といえる.
技術的な側面からみたCHAMPの特徴として,まず,一つはH-Lトラッキング用の受信機として新たに開発されているTurbo-Rogueの受信機が使用されることであり,この受信機は,今後,Jason-1の精密軌道決定やGRACEミッションでも利用される予定であり,その性能に注目されている.また,H-L SSTによる重力場の測定において一つの重要な問題は,衛星軌道における残留大気の抵抗や太陽輻射,その他の原因による軌道の乱れの影響である.これらは,通常,地球の重力場の空間的変化より大きいため,その影響を何らかの形で補正しないかぎり重力場のシグナルを得ることは不可能である.このため,CHAMPでは,別途,衛星の重心付近に加速度計(Accelerometer)を搭載し,衛星軌道における重力場以外の原因による加速度変化の補正が可能なように設計されている.
CHAMPによる重力場の測定は,その主な目的が,次期の衛星高度計搭載衛星であるJason-1の精密軌道予測のための重力場の改良にあり,期待できる精度は,Fig.4に示すように,次数30次程度の球関数係数にして,現存する最良のモデル(EGM96)より半桁程度の改良に留まっている.しかし,衛星軌道から直接重力場を測定する試みは,CHAMPミッションが歴史上初めてであることや,先に述べたように,CHAMPミッションで使用されるのと同じタイプのGPS受信機や加速度計を用いたH-L SSTは,次に述べるGRACEミッションでも使用される予定であり,CHAMPの成否は,Jason-1やGRACEなど,今後の衛星計画にも大きな影響をおよぼすものと思われる.
3.4.GRACEミッション
GRACEミッションは,NASAとGFZ(GeoForschungsZentrum)が共同で進めている本格的な重力測定ミッションであり,現在,2001年6月の打ち上げが予定されている.GRACEミッションでは,重力場の測定原理としては,いわゆるLow-Low Satellite-to-Satellite Tracking (L-L SST)と呼ばれる技術が用いられる.L-L SSTは,比較的低高度(300〜400km)の同一軌道に数100kmの間隔で2つの衛星を打ち上げ,衛星間の距離の変化(range rate)をマイクロ波干渉計で極めて精密に計測するものであり,その精度は,GRACEでは1μm/secより良いと見積もられている.ここでの衛星間の距離変化の測定とは,すなわち衛星軌道における速度を測定していることであり,従って,その1階微分として重力加速度を求めることができる.なお,L-L SSTとしては,衛星間の測距手段として,GRACEのようにマイクロ波レーダーを使うタイプの他に,レーザー光による干渉測位を用いることも考えられている.レーザー干渉測位によるSSTを用いた衛星重力ミッションは,現状では,まだ技術的にさまざまな困難が伴うものの,レーダーに比べさらに1桁程度の精度向上が望めることから,将来の計画が期待される.
GRACEミッションでは,処理レベルが異なる幾つかの種類のデータセットが提供されることになるものと予想されるが,最終段階のものとしては,次数(n)が100次程度までの重力場の球関数展開係数が,例えば,一月に1回程度の頻度で公開されるものと思われる.この場合,予想される重力場の精度としては,Fig. 4に示すように現存する最良の地球重力場モデルEGM96と比較して1〜3桁も高いと見積もられており,これが実現すると,海面高測定の基準としての静的なジオイド面の決定はもちろん,さらに興味深いのは,従来は静的と考えていたジオイド面そのものの時間変化までもが検出可能になることである.
地球レベルでの重力場の時間的変化の原因としてまず考えつくのが,地球表面の流体部分の運動による質量の再配分であり,GRACEミッションに関連して成果の期待される研究課題としても,海洋における熱・質量輸送に関する研究,全球的な水収支に関する研究,海水準変動に関する研究,氷床や氷河の進退に関する研究,大気質量変動に関する研究などがあげられている(National Research Council, 1997).従来,これらの影響は,VLBI,SLR,GPSによる地球回転の観測やSLRによる衛星追跡データから,ごく低次の球関数係数の時間的変化は観測されていたが(例えば,Chao and Au, 1991; Chen et al., 1997),GRACEミッションが実現した際には,Fig.4の単純なS/N比の見積もりでは,波長1000km程度より長波長の現象については,海洋や陸水の年周的な質量移動に関連した重力変化の分離も十分可能であると思われる.さらに,地球表面の流体部分の影響以外にも,その空間的変動パターンの違いから,氷河後退後のアイソスタシー回復に伴う重力変化なども検出が可能であると期待されており,これらの情報は,例えば,マントル物質の粘性率の見積もりなどにも強い拘束条件を与えることになるであろう.
3.5.衛星重力ミッションと地上の重力観測
GRACEミッションが実現すると,かつてなかった高精度の重力変化データが得られることになる.このような高精度のデータは歴史上存在しなかったわけであり,地上の観測においてさえ,現在,この精度に匹敵しうるのは超伝導重力計や絶対重力計による観測ぐらいである.しかしながら,GRACE衛星によって観測される重力場データと地上での超伝導重力データでは,その空間的,時間的分解能が全く異なっている.さらに,地上での重力観測と衛星での観測では,同じ原因に対する重力変化の見え方も異なってくる.例えば,海洋の加重変形に対する重力の変化を考えても,地上の観測においては,変形による観測点そのものの上下動の影響も考慮する必要があるが,衛星軌道での観測においては,地球の変形による質量再配分の効果だけを考慮すればよい.また,大気の変動に関しては,地上と衛星観測では大気層の内部か外部かといった根本的な違いが生じる.従って,衛星測定による重力と超伝導重力を一対一に比較することはほとんど不可能であり,どのようなキャリブレーションの方法があるか,それ自体,今後の重要な研究課題となっている.このような問題への一つのアプローチとして,重力変化を引き起こすそれぞれの現象について,その現象をモデル化し,モデルを介した現象の再現が陸上ならびに衛星軌道レベルで可能かどうかを検証する方法が考えられる.Wahr and Molenaar (1998)は,GRACEミッションを想定した衛星軌道レベルでのこのようなデータのシミュレーションを行っているが,今後,同様のシミュレーションを陸上観測を想定して実施することも必要があろう.
一方,現在の精密重力測定における問題の多くは,実は,地球表面における流体部分の運動が測定ノイズとして入ってきていることに起因している.例えば,超伝導重力観測における気圧変動の影響についてはすでに多くの研究があるが(例えば,Mukai et al, 1995),さらに,最近では,長周期の海洋変動が重力変動に及ぼす影響についても研究されるようになっている(例えば,Fukuda and Sato, 1997).精密重力観測の立場からみた衛星重力ミッションの意義の一つは,このような種々の影響が衛星重力観測によって直接観測出来るようになることである.すなわち,従来,問題となっていた環境変動によるノイズ成分の一部は,今後,実測値として補正出来る可能性が出てきている.もちろん,この場合にも上記と同じ理由で,種々の影響を一対一に補正することはほとんど不可能であろうが,現象の適当なモデリングによってこのようなことも可能であろう.何れにしろ,陸上,衛星を問わず,現在の精密重力測定の精度は,種々の現象の地球規模での総合的な理解を要求していることはあきらかである.
4.おわりに
衛星高度計による海域重力場の研究から海洋変動の研究,さらに今後の重力ミッションについて概観した.衛星高度計の成果やGRACE計画などをみると,これらがもはや重力場の研究という枠組みではとらえきれなくなっていることは明白である.あるいは,現代測地学そのものが,その対象とする現象について,従来一般に考えられていたような固体地球物理学の一分野としての枠組みを完全に越えており,それを包含するかたちで,流体部分を含む地球全体の計測科学として進展していると言えるであろう.
衛星重力ミッションの可能性や重要性については既に述べたとおりであるが,衛星重力測定データを最大限に活かし,地球科学的に意味のある情報を引き出すためには,他の観測量との結合が何よりも重要である.例えば,衛星高度計データと衛星重力データを組み合わせることにより海洋における質量輸送の情報が得られ,さらにそれは,地上での精密重力測定に依って検出可能なはずである.このように,衛星と地上観測のリンクについてはさまざまなシナリオが考えられており,これらは,やはり今後の重要な研究課題であろう.特に,今後の衛星重力ミッションにおいてその精度やパフォーマンスを調べる上でも,地上での重力測定データとの比較が極めて重要な課題である.我が国は,多数の超伝導重力計や絶対重力計を保有しており,このようなground truthは,観測的手法として,現時点で我が国が国際的に貢献しうる重要な課題の一つであろう.
文献
Chao, B.F. and A. Y. Au (1991): Temporal variation of Earth's zonal gravitational field caused by atomospheric mass redistribution: 1980-1988, J.Geophys. Res., 96, 6569-6575.
Chen, M.K., C.K. Shum and B. D. Tapley (1997): Determination of long-term changes in the Earth's gravity field from satellite laser ranging observations, J.Geophys. Res.,102, 22377-22390.
Cheney, R. E., B. C. Douglas, R. W. Agreen, L. Miller, D. Milbert and D. L. Porter; The GEOSAT Altimeter Mission (1986): A Milestone in Satellite Oceanography, EOS, 67, 1354-1355.
Fukuda, Y., J. Segawa, H. Watanabe and A. Iwasita (1988): GEOSAT Altimeter Data Processing, J. Geod. Soc. Japan, 34, 97-108.
福田洋一(1995): 日本およびその周辺のジオイドの精密決定,測地学会誌,41,1-16.
Fukuda, Y., and T. Sato (1997): Gravity effects of sea level variation at the superconducting gravimeter sites, estimated from ERS-1 and TOPEX/Poseidon altimeter data, IAG Symposia 117, Segawa et al. (eds.), GraGeoMar, Tokyo, Japan,Sep.30-Oct.5, 1996,107-114.
Fukuda, Y., J. Kuroda, Y. Takabatake, J. Itoh and M. Murakami (1997):Improvement of JGEOID 93 by the geoidal heights derived from GPS/Leveling survey, IAG Symposia 117, Segawa et al. (eds.), GraGeoMar, Tokyo, Japan,Sep.30-Oct.5, 1996, 589-596.
Haxby, W. F. (1987): Gravity Field of the World's Ocean, NODC, NOAA.
Heiskanen, W. and H. Moritz(1967): Physical Geodesy, W. H. Freeman and Company, San Francisco, 1-364.Jekeli C. and T. N. Upadhyay (1990) : Gravity estimation from STAGE, a Satellite-to-Satellite Tracking Mission, J. Geophys. Res., 95, 10973-10985.
Knudsen, P. and O. B. Andersen (1994): Global Analysis of the Gravity Field From the First Repeat of the ERS-1 Geodetic Mission, EOS trans. AGU,75, No.44, p 155.
Lemoine, F.G., S.C. Kenyon, J.K. Factor, R.G. Trimmer, N.K. Pavlis, D.S. Chinn, C.M. Cox, S.M. Klosko, S.B. Luthcke, M.H. Torrence, Y.M. Wang, R.G. Williamson, E.C. Pavlis, R.H. Rapp and T. R. Olson (1998): The Development of the Joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) Geopotential Model EGM96, NASA/TP-1998-206861, 575p.
Lerch, F. J., J. G. Marsh, S. M. Klosko and P. G. Williamson(1982): Gravity Model Improvement for SEASAT, J. Geophys. Res., 87, 3281-3296.
Liang C.-K. (1983): The Adjustment and Combination of Geos-3 and Seasat Altimeter data, Dep. of Geod. Sci., Ohio State Univ. Rep. 346, 1-68.
Matsumoto, K., M. Ooe, T. Sato and J. Segawa (1995): Ocean tide model obtained from TOPEX/POSEIDON altimetry data, J. Geophys. Res., 100, 25319-25330.
Mukai, A., T. Higashi, S. Takemoto, I. Nakagawa and I. Naito (1995): Accurate Estimation of Atmospheric Effects on Gravity Observations Made with a Superconducting Gravity Meter at Kyoto, Phys. Earth Planet Inter., 91, 149-159.
Morel, L. and P. Willis(1999): Systematics effects of terrestrial reference frames on mean sea level determinations, Poster presented at TOPEX/Poseidon, JASON-1 SWT meeting, Saint Raphael, Oct. 25-27, 1999.
NASA (1987) : Geophysical and Geodetic Requirements for Global Gravity Field Measurements 1987-2000, Report of a Gravity Workshop Colorad Springs, Colorad February 1987, 1- 45.
National Research Council (1997): Satellite gravity and the geosphere, National Academy Press Washington, D.C., 1-112.
Nerem, R.S., B.J.Haines, J. Hendricks, J.F. Minster, G.T. Mitchum and W.B.White(1997): Improved determination of global mean sea level variations using TOPEX/POSEIDON altimeter data, Geophysical Research Letters, 24, 1331-1334.
Rapp, R. H. (1979): Geos 3 Data Processing for the Recovery of Geoid Undulations and Gravity Anomalies, J. Geophys. Res., 84, 3784- 3792.
Rapp, R. H. (1981): The Earth's Gravity Field to Degree and Orger 180 Using SEASAT Altimeter Data, Terrestrial Data and Other Data, Dep. of Geod. Sci. Ohio State Univ., Rep. 334.
Rapp, R.H. (1985): Detailed Gravity Anomalies and Sea Surface Heights Derived From Geos-3/Seasat Altimeter Data, Dep. of Geod. Sci., Ohio State Univ., Rep. 365.
Rapp, R.H. and J. Y. Cruz(1986): Spherical Harmonic Expansions of the Earth's Gravitational Potential to Degree 360 Using 30' Mean Anomalies, Dep. of Geod. Sci., Ohio State Univ., Rep. 376.
Rapp, R.H. and Palvis N. K. (1990): The Development and Analysis of Geopotential Coefficient Models to Spherical Harmonic Degree 360, J. Geophys. Res., 95, 21885-21911.
Rapp, R.H., Y.M. Wang and N. K. Pavlis (1991): The Ohio State 1991 Geopotential and Sea Surface Topography Harmonic Coefficient Models, Dep. of Geod. Sci., Ohio State Univ., Rep. 410, 94p.
Rowlands, D. (1981): The Adjustment of Seasat Altimeter Data on a Global Basis for Geoid and Sea Surface Height Determinations, Dep. of Geod. Sci., Ohio State Univ., Rep. 325.
Sandwell, D. T. (1984): A Detailed View of the South Pacific Geoid From Satellite Altimetry, J. Geophys. Res., 89, 1089-1104.
Sandwell, D. T. and W.H.F. Smith (1997): Marine gravity anomaly from Geosat and ERS-1 satellite altimetry. J. Geophys. Res., 102, 10039-10054.
Segawa, J., and T. Asaoka (1982): Reevaluation of Geoid based on the SEASAT altimeter data - Goeid around Antarctica -, J. Geod. Soc. Jpn, 28, 162-171.
Segawa, J., Matsumoto, T. and K. Kaminuma (1984): Free air gravity anomaly of Antarctic region, Spec. Map Ser. Natl. Inst. Polar Res., No. 3.
Segawa, J. and T. Matsumoto (1987): Free Air Gravity Anomaly of the world Ocean as Derived From Satellite Altimeter Data, Bull. Ocean Res. Inst., Univ. of Tokyo, 25.
UT-CSR (1998): CRACE Preliminary Design Review, University of Texas, Center for Space Research, Austin, 19-20 August, 1998.
Wahr, J. and M. Molenaar (1998): Time variability of the Earth's gravity field: Hydrological and oceanic effects and their possible detection using GRACE, J. Geophys. Res., 103, 30205-30229.
Zuffada, C., H. George and J. B. Thomas (1999): A novel approach to ocean altimetry utilizing the GPS signal, Abstract of International Symposium on GPS in Tsukuba, 1999, 07-07.
Fig. 1. A schematic view of the satellite altimetry.
Fig. 2. A schematic view of the sea surface dynamic topography which is caused by geostrophic balance between ocean current and the slope of the sea surface.
Fig.3. Summary of requirements for gravity measurement accuracy as a function of spatial resolution. (after NASA 1987)
Fig.4. Geoid uncertainty in EGM96 vs predicted GRACE mission (after UT-CSR, 1998). The curve for CHAMP mission is added using the data from NRC (1997).
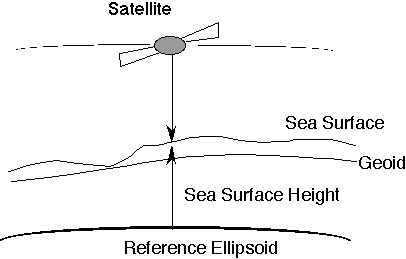
Fig. 1. A schematic view of the satellite altimetry.

Fig. 2. A schematic view of the sea surface dynamic topography which is caused by geostrophic balance between ocean current and the slope of the sea surface.
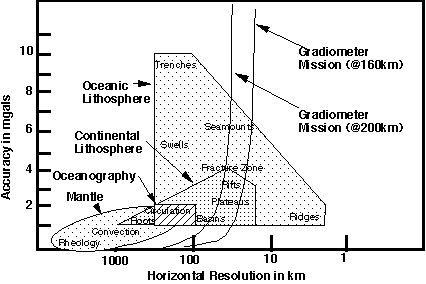
Fig.3. Summary of requirements for gravity measurement accuracy as a function of spatial resolution. (after NASA 1987)
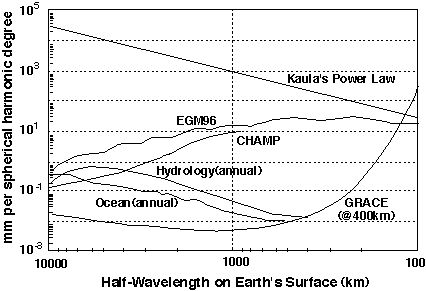
Fig.4. Geoid uncertainty in EGM96 vs predicted GRACE mission (after UT-CSR, 1998).
The curve for CHAMP mission is added using the data from NRC (1997).