陸水流動に伴う重力擾乱の水文学的モデリング
重力観測を用いて地殻変動や火山活動を把握する際には、陸水流動による重力擾乱を適切に補正する必要があります。 私は水文学の物理方程式を用いて陸水擾乱をモデル化し、数マイクロガルの精度で陸水擾乱を再現することに成功しました。
(記事作成日:2016年9月2日)
陸水流動に伴う重力擾乱
重力加速度は質量分布の空間積分によって表現できるので、重力観測によって地殻変動や火山活動をモニターすることができます。
しかしながら、重力は水質量の移動(例えば降水や地下水流動など)によっても変化します。
半無限媒質上に1mmの降雨があった時の重力変化は0.042マイクロガル/mmとなりますが、実際の地形は半無限媒質で近似できませんし、降雨後の水の移動は非常に複雑です。
陸水起源の重力擾乱は50年以上前からその存在が指摘されていたにもかかわらず、その物理学的解釈は近年まで不十分でした。
私は大学院修士課程以降、この問題について研究してきました。
その結果、地中の陸水流動をフォワードでモデル化することにより、陸水擾乱を再現できることが分かりました。
以下では、3つの陸水擾乱モデルについて紹介し、今後の展開を述べます。
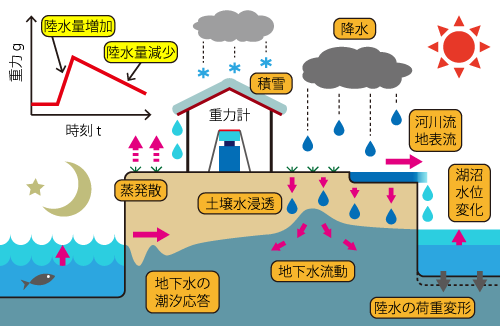
図1 : 陸水起源の重力擾乱に関する概念図
3次元陸水モデル G-WATER [3D] による重力擾乱の再現
地表下は、土壌空隙に水と空気が含まれている「不飽和層」と、土壌空隙が水で満たされている「地下水帯水層」が重なり合っています。 私が作成した3次元陸水モデル G-WATER [3D] では、不飽和層と不圧地下水帯水層の水質量分布を水文学の物理方程式に則して時空間的に数値計算し、これを空間積分することで重力変化を見積もります。 境界条件や土壌パラメーターの設定に労力を要したものの、浅間山では絶対重力計FG5の重力連続データを3マイクロガルの精度で再現することに成功しました。 また、浅間山と桜島の噴火時には、重力観測データから陸水擾乱計算値を差し引くことで、火山活動起源の重力変化(それぞれ5および10マイクロガル)を抽出することに成功しました。
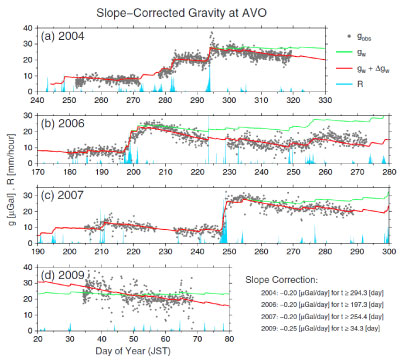
図2 : G-WATER [3D] によって再現された浅間山の陸水重力擾乱
鉛直1次元陸水モデル G-WATER [1D] による重力擾乱の再現
「地表形状が半無限媒質で近似できる」「重力観測点直下の地下水位データが得られている」という特別な場合には、不飽和層内の土壌水の時空間分布をモデル化するだけで重力擾乱を再現可能です。 G-WATER [1D] はそのための陸水モデルであり、岩手県の胆沢扇状地に対して適用実験がなされました。 その結果、超伝導重力計SGで観測された2年間(2009-2010年)の重力変化を約1マイクロガルで、50日間の重力変化に至っては0.4マイクロガルという高精度で再現可能であることが分かりました。 なお、試行実験直後の2011年3月には東北地方太平洋沖地震が発生したため、地震前後の重力観測データに本モデルを適用すれば地殻変動に伴う重力変化を抽出できるかもしれません。
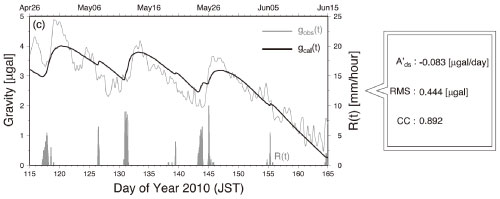
図3 : G-WATER [1D] によって再現された胆沢扇状地の陸水重力擾乱
経験的陸水モデル G-WATER [E] による重力擾乱の再現
上記2つの陸水モデルは陸水流動の物理法則を用いてモデル化しているので、陸水分布や重力擾乱を精度よく再現できます。 一方で、土質試験によって土壌パラメーターを予め実測する必要があるなど、水文学的技能がなければモデルを使いこなせない、というデメリットもあります。 私はこの点に注目し、「重力擾乱の再現精度は低くてもいいから、経験的にかつ簡便に重力擾乱を再現する」という手法を開発しました。 G-WATER [E] がその陸水モデルであり、桜島に適用したところ約8マイクロガルの精度で重力連続データを再現できました。 この結果は、G-WATER [E] を用いた絶対重力データ(観測精度:約2マイクロガル)の陸水擾乱補正は難しいものの、相対重力データ(観測精度:約10マイクロガル)の簡易的な陸水補正には有効であることを示しています。 実際、この陸水モデルは桜島で観測された相対重力変化の特徴をよく再現しています。
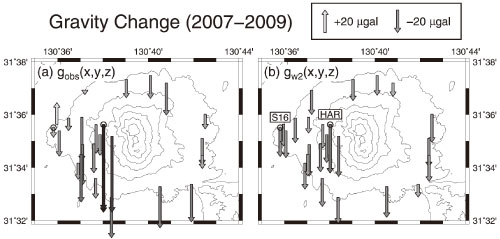
図4 : 桜島で観測された重力変化(左)とG-WATER [E] によって再現された陸水重力擾乱(右)
今後の展開
上記3つの陸水モデルは、基本的にはどんな場所にでも適用可能です。 すなわち、入力データ・境界条件・媒質パラメーターなどを適切に設定すれば、あらゆる場所の陸水重力擾乱を再現することができます。 ただし、これらのモデルはフォワード計算を行っているに過ぎないので、計算結果と観測データの比較により条件設定を試行錯誤的に修正していく必要があるかもしれません。 この問題を解決するには、データ同化によってモデルパラメーターを推定していく手法が有効と考えられますが、私自身はまだ着手していません。 逆問題(インバージョン)的に陸水擾乱を簡単に再現することができれば、重力観測を用いた固体地球変動の研究がさらに発展すると期待されます。

図5 : 国土地理院(茨城県つくば市)における土壌サンプル採取の様子
関連論文・リンク
- 風間卓仁 (2015): 地上重力測定における陸水擾乱問題. In: 日本測地学会(編), 測地学テキストWeb版. LINK
- T. Kazama and S. Okubo (2009): Hydrological modeling of groundwater disturbances to observed gravity: Theory and application to Asama Volcano, Central Japan. J. Geophys. Res. (Solid Earth), 114 (B8), B08402, doi:10.1029/2009JB006391. LINK
- T. Kazama, S. Okubo, T. Sugano, S. Matsumoto, W. Sun, Y. Tanaka, E. Koyama (2015): Absolute gravity change associated with magma mass movement in the conduit of Asama Volcano (Central Japan), revealed by physical modeling of hydrological gravity disturbances. J. Geophys. Res. (Solid Earth), 120 (2), 1263-1287, doi:10.1002/2014JB011563. LINK
- T. Kazama, Y. Tamura, K. Asari, S. Manabe, S. Okubo (2012): Gravity changes associated with variations in local land water distributions: observations and hydrological modeling at Isawa Fan, northern Japan. Earth Planets Space, 64 (4), 309-331, doi:10.5047/eps.2011.11.003. LINK
- 風間卓仁, 山本圭吾, 福田洋一, 井口正人 (2014): 相対重力データに対する陸水擾乱補正の重要性:桜島火山を例に. 測地学会誌, 60 (2), 73-89, doi:10.11366/sokuchi.60.73. LINK
- G-WATERのページ
